Tüpte sıvı: sorular ve cevaplar
Bu yazının konusu boruda sıvıdır. Hareketini, hızını ve hacmini tanımlayan fiziksel yasa ve formülleri tanımak zorundayız. Karmaşık hesaplamaların doğuşuna girmemeye çalışacağız: bizim görevimiz, hidrodinamikten uzak bir insan için hesaplama için anlaşılabilir ve erişilebilir olacak kalıpları tanımlamaktır.
Hadi başlayalım.

boyutlar
çap
Su ve gaz boruları durumunda, oldukça sıradan bir ölçüm sistemi ile uğraşıyoruz. İlgili boru hatları için, ana parametre olarak koşullu geçiş veya nominal çapın (DU) biraz olağandışı konsepti kullanılır. Hem inç hem de milimetre cinsinden ölçülür; Aynı VGP borusu 1 1/4 inç veya DU32 mm olarak satılabilir.
Referans: bu durumda uzunluk ölçüsü olarak, ingiliz inç, 2.54 santimetre eşit kullanılır. İnç milimetre olarak dönüştürülürken, GOST tarafından sağlanan nominal çapların adımı dikkate alınmalıdır; Bu durumda, yukarıdaki durumda, 1 1/4 inçlik bir milimetreye basit bir yeniden hesaplama 32, ancak 1.25x2.54 = 31.75 mm verecektir.
GOST 3262-75 tarafından öngörülen su ve gaz borularının boyutlarını veriyoruz.
| Koşullu geçiş (DU), mm | Gerçek dış çapı, mm |
| 15 | 21.3 |
| 20 | 26.8 |
| 25 | 33.5 |
| 32 | 42.3 |
| 40 | 48.0 |
| 50 | 60.0 |
| 65 | 75.5 |
| 80 | 88,5 |
| 90 | 101.3 |
| 100 | 114.0 |
| 125 | 140.0 |
| 150 | 165.0 |
Duvar kalınlığı aynı büyüklükte (borular hafif, sıradan ve takviyeli) değiştiğinden, DU'nın genellikle iç çapa yakın olduğunu, ancak kural olarak ona eşit olmadığını söyleyebiliriz.

bölüm
Su borularının yapımında, nadir istisnalar dışında yuvarlak borular kullanılmaktadır.
Bunun için iki çok iyi sebep var.
- Yuvarlak boru, enine kesit alanına sahip minimum duvar alanına sahiptir.. Bu nedenle, sabit bir duvar kalınlığına sahip boru hattının metre başına fiyatı minimum olacaktır - sadece daha düşük malzeme tüketimi nedeniyle.
- Maksimum çekme mukavemeti için yuvarlak kesit. Gerçek şu ki, duvarlara karşı aşırı baskı yapan iç ortamın kendi bölgeleriyle doğru orantılı olduğu güç; ve zaten öğrendiğimiz gibi, alan sadece yuvarlak boruda en azdır.

İç kesit alanı S = Pi * R ^ 2 formülü kullanılarak hesaplanır, burada S istenen alan değeridir, Pi pi sayısıdır, yaklaşık olarak 3.14159265'e eşittir ve R yarıçapıdır (iç çapın yarısı). Örneğin, iç çapı 200 mm olan bir boru için, bölüm 3.14159265x (0.1 ^ 2) = 0.031 m2 olacaktır.
Dairesel bir borudaki bir akışkanın akışı her zaman tüm hacminin dolmasıyla ilişkili olmadığı için, hesaplamalarda genellikle bir yaşam bölümü kavramı kullanılır. Akış alanı denir. Örneğin, bir boruyu tam olarak doldururken, (Pi * R ^ 2) / 2'ye eşittir (yukarıdaki örnekte, 0.031 / 2 = 0.00155 m2).
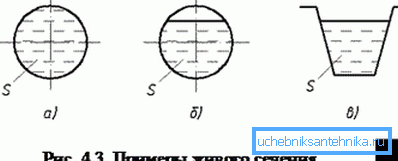
hacim
Borudaki sıvı hacminin ne olduğunu bulalım. Geometri açısından, herhangi bir boru bir silindirdir. Hacmi kesit alanın ve uzunluğun ürünü olarak hesaplanır.
Böylece, 0.031 m2 kesit alanına sahip, tam dolu bir boru hattındaki 8 metre uzunluğundaki sıvı hacmi 0.031x8 = 0.248 m3'e eşit olacaktır.
Kısmen doldurulmuş bir boru için, ortalama canlı bölüm hesaplama için kullanılır. Sabit bir eğim ve akış ile, borulardan akışkanın hareketi tekdüze olacaktır; buna göre, yaşam bölümü basınçsız boru hattının tüm bölümlerinde aynı olacaktır.
tüketim
Borunun içinden sıvı akış oranının nasıl hesaplandığını anlayacağız. Görevin büyük bir pratik değeri vardır: Su boru hatlarının bilinen sayıda sıhhi tesisat armatürü ile hesaplanmasıyla doğrudan ilgilidir.
Basit ve evrensel bir hesaplama yöntemi olmadığı için üzülmeniz gerekir. Neden?
Sadece kendi ellerinizle tam bir hidrodinamik hesaplama yaparken çok sayıda faktörü göz önünde bulundurmanız gerekir:
- Borunun iç yüzeyinin sürtünme katsayısı. Açıkçası, kaba, tortu kaplı çelik, suyun hareketine yumuşak polipropilenden çok daha fazla direnç sağlayacaktır.

- Boru hattının uzunluğu. Sıvıdan geçecek mesafe ne kadar büyük olursa, duvarlara doğru akış yavaşlaması nedeniyle basınçtaki düşüş o kadar büyük olur ki, tüketimdeki azalma o kadar güçlü olur.
- Boru hattı çapı, borulardan viskoz akışkan akışını, göründüğünden çok daha karmaşık bir şekilde etkiler. Enine kesit ne kadar küçük olursa, borunun akışı o kadar büyük olur. Bunun nedeni, çap azaldıkça, iç hacminin ve duvar alanının oranının değişmesidir.
Dikkat edin! Kalın bir boru hattında, duvarlara en yakın olan derenin bir kısmı içeride bir tür yağlayıcı görevi görür. İnce bir tabakada, bu yağın kalınlığı yetersizdir.
- Son olarak, boru hattının her dönüşü, çapın geçişi, kapama valfinin her elemanı da akış hızını etkileyerek akış hızını yavaşlatır.

Tüm bu faktörlerin sonucu birkaç yüzde etkilemediği anlaşılmalıdır: örneğin, cilalı bir iç yüzeyli ve aşırı büyümüş tortular için (lümen içindeki düşüş hesaba katılmadan bile) yeni bir çelik boru için hidrodinamik direnç 200 kattan fazla farklılık gösterir.
Tam konfigürasyon, malzeme ve yaş hesaba katılarak boru hattının hidrolik hesaplaması için gerekli olan tüm profesyoneller, F.A. Sheveleva. Bu tablolara dayanarak, çeşitli derecelerde güven ile hesaplamalar yapmanızı sağlayan birçok çevrimiçi hesap oluşturulmuştur.
Bununla birlikte, bağımsız hesaplamaları önemli ölçüde basitleştirmenize izin veren bir boşluk vardır. Deliğin içinden akışkan akışında, sıvı besleme borusuyla karşılaştırıldığında göz ardı edilebilir (ki bu, çoğu sıhhi tesisat cihazı ile çalışırken gerçekte gözlemliyoruz), Torricelli'nin yasası geçerlidir.
Bu kanuna göre, tarif edilen durumda, V ^ 2 = 2gH formülü, ki burada V delikteki akış hızıdır, g yerçekiminin ivmesidir (9.78 m * s ^ 2) ve H deliğin üstündeki sütunun yüksekliği veya bir şeydir. aynısı, onun önünde baskı.
Referans: 1 atmosfer (1 kgf / cm2), 10 metrelik bir su kolonunun basıncına karşılık gelir.
Delikteki akış oranı akışla nasıl ilişkilidir? Bizim durumumuzda, hesaplama talimatı basittir: S ürününe eşit bir sıvı hacmi ve akış oranı V, kesit alanı S ile delikten geçecektir.
Örnek olarak, su basıncını, 10 metrelik bir basınçta 2 santimetre çapındaki bir delikten, aşırı basınç atmosferine tekabül eden bir delikten hesaplayalım.
- V ^ 2 = 2 x 9.78 * 10 = 195.6
- V, 195.6'nın kareköküne eşittir. Hesaplama kolaylığı için sonuç (13.985706 m / s), 14 m / s'ye yuvarlanır.
- Yukarıdaki formüle göre iki santimetrelik bir çapa sahip deliğin kesit alanı 3.14159265 * 0.01 ^ 2 = 0.000314159265 m2'dir.
- Bu nedenle, gider, 0.000314159265 * 14 = 0.00439822971 m3 / s'ye eşit olacaktır. Kolaylık sağlamak için bunu litre haline getireceğiz: 1 metreküp 1000 litreye eşit olduğu için, kuru kalıntıda saniyede 4,4 litre sonuç alınacaktır.
Tamlık için, bazı referans verileri sunuyoruz.
| Sıhhi tesisat armatürü | Ortalama su tüketimi, l / s |
| Su musluğu ile lavabo | 0.1 |
| Lavabo bataryası | 0.12 |
| Karıştırıcı ile lavabo | 0.12 |
| Küvet mikserli | 0.25 |
| Mikser ve havalandırıcı ile bide | 0.08 |
| Klozet | 0.1 |
| Bulaşık makinesi (su seti) | 0.3 |
| Otomatik çamaşır makinesi | 0.25 |
Akış hızı
Borudaki akışkan debisinin hesaplanması nedir? Küçük çaplı bir delikten dışarı akması durumunda, yukarıdaki Torricelli yasası geçerlidir.
Bununla birlikte, çoğu durumda, borudaki sıvının akış hızı, hidrolik direnci ihmal edilemeyen uzun bir boru hattı için hesaplanır. Eğer öyleyse - aynı problemlerle karşılaşırız: çok sayıda faktör, bölümü sabit bir farkla hıza etkiler.
Giderimizi biliyorsak durum büyük ölçüde basitleştirilmiştir. Sıkıştırılamayan sıvılar için, süreklilik denklemi için basitleştirilmiş bir formül geçerlidir: Q = Av, Q, saniyede metre cinsinden su akışıdır, A, tam veya yaşayan bölümün alanıdır, v, dairesel kesitli bir borudaki veya başka herhangi bir formdaki bir sıvının ortalama hızıdır.
Su tüketiminin yukarıdaki referans verilerini sıhhi teçhizat ile bilmek, bilinen bir çaptaki bir su borusu içindeki akış hızını hesaplamak kolaydır.
Örnek olarak, bir bulaşık makinesi ve lavabo kullanarak, drenaj tankını doldururken, 15 mm'lik (0,015 m) bir iç çapı olan suyun soğuk su besleme borusunda ne kadar hızlı hareket edeceğini öğrenelim.

- Cihazların toplam su tüketimi, yukarıdaki tabloya göre, 0,1 + 0,3 + 0,12 = 0,52 l / s veya 0,00052 m3 / s olacaktır.
- Borunun kesit alanı 3.14159265 x 0.0075 m ^ 2 = 0.000176714865625 m2'dir.
- Saniyede metre cinsinden akış hızı 0.00052 / 0.000176714865625 = 2.96'dır.
Referans olarak, çeşitli amaçlar için boru hatlarında su hızının bazı değerlerini veriyoruz.
| sistem | Hız aralığı, m / s |
| Yerçekimi ısıtma sistemi | 0.2 - 0.5 |
| Zorla dolaşım, şişeleme ile ısıtma sistemi | 0,5 - 3 |
| Zorlanmış sirkülasyonlu ısıtma sistemi, ısıtma cihazlarına bağlantılar | 0.2 - 0.5 |
| Su şebeke | 0,5 - 4 |
| Su kaynağı | 0,5 - 1 |
| DHW sisteminde sirkülasyon | 0.2 - 0.5 |
| Serbest akışlı kanalizasyon (fırtına kanalizasyon dahil) | 0,35 - 1 |
Yararlı: 1,5 m / s'ye kadar akış hızı rahat olarak düşünülür ve boru hattı duvarlarının aşındırıcı erozyonunun hızlanmasına neden olmaz. 2,5 m / s hıza kadar geçici bir artış kabul edilebilir.
Çap ve basınç
Bir akışkanın bir borudaki davranışının bir başka ilginç yönü, akış hızı ve içindeki statik basınç arasındaki ilişkidir. Bernoulli yasası tarafından tarif edilmiştir: statik basınç akış hızı ile ters orantılıdır.
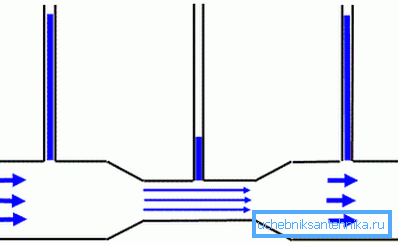
Bu yasanın pratik uygulaması birçok modern mekanizmada somutlaşmıştır.
İşte sadece birkaç örnek:
- Pnömatik püskürtme tabancası, tam olarak boyayı depodan emen ve boyalı yüzeyde portatif bir aerosole dönüştüren hava jetinde oluşan nadir bir durum nedeniyle çalışır.
- Isıtma ana hattına bağlı bir evin asansör ünitesinde, besleme borusundan nozul tarafından yaratılan suyun jetindeki vakum, geri dönüşten tekrarlanan sirkülasyon döngüsüne suyun emme kısmı boyunca çekilir.

Sonuç
Okuyucumuzun küçük gezimizi fizik, geometri ve hidrodinamik temellerini çok yorucu bulmadı. Her zaman olduğu gibi, bu makaledeki videoda ek tematik bilgiler bulunabilir (ayrıca bkz. Bacalar: Kurulum ve Bakım).
İyi şanslar!